INTRODUCCIÓN
El ser humano ha sentido a lo largo de la historia un elevado interés por el número áureo, asociándolo con el ideal de belleza y otorgándole una importancia mística.
El número áureo se encuentra omnipresente en nuestras vidas, tanto en la propia naturaleza, en la que se presenta de manera sorprendente y realmente fascinante, como como en las creaciones realizadas por el hombre. Dada su ubicuidad, el número áureo es a menudo considerado como el huevo de Pascua de la naturaleza, ya que parece haber sido escondido por todas partes a la espera de ser descubierto en cualquier momento por aquellos que quieran observar e investigar.
Sus propiedades algebraicas y geométricas le dotan de unas especiales características de autosimilitud (autosemejanza) que resultan cruciales para la importancia del número áureo.
El número áureo ha inspirado a pensadores de todas las disciplinas como ningún otro número en la historia de las matemáticas.
EL NÚMERO ÁUREO
El número áureo es un número irracional que representa una proporción concreta entre dos cantidades. Ha recibido a lo largo de la historia otros muchos nombres, entre los que destacan: razón medios y extremos; razón áurea; áurea mediática; razón dorada; número de oro; proporción áurea; número de Dios; y divina proporción.
Aunque antiguamente se representaba con las letras griegas tau o alfa, en la actualidad es muy común representarlo mediante la letra griega phi, tanto en mayúscula como en minúscula.
HISTORIA
En la antigüedad, el número áureo se descubrió como un concepto geométrico, no como una expresión aritmética. A lo largo de la historia este número, cuyo descubrimiento se debió a la geometría, ha recibido diversas denominaciones, haciendo referencia a su origen geométrico (razón, proporción), ya su relación con la belleza (áureo, dorado) y la divinidad (divino, de Dios).
Se cree que el número áureo se encuentra como proporción en varias estelas de Babilonia y Asiria de alrededor del 2.000 aC Sin embargo, no existe documentación histórica que acredite que dicho número fuera empleado de forma consciente en la elaboración de las estelas, por lo que no se sabe si la aparición del número áureo en la medición de las proporciones de dichas estelas fue intencionada (conociendo por tanto la proporción) o casual (desconociéndola).
El primer estudio formal sobre el número áureo del que se tiene constancia (alrededor del 300 aC) se debe a Euclides, considerado el padre de la geometría. En su tratado 'Los Elementos', concretamente en la Proposición 30 del Libro Sexto de dicho tratado, Euclides definió al número áureo de
De la siguiente manera:
'Se dice que una recta ha sido cortada en extrema y media razón cuando la recta entera es al segmento mayor como el segmento mayor es al segmento menor'
Euclides también demostró que este número no puede ser expresado o descrito como la razón de dos números enteros, es decir, que es un número irracional.
Ya en la Edad Media, Abu Kamil (850-930) realizó cálculos geométricos en pentágonos y decágonos usando el número áureo.
En el Renacimiento, en 1509 el matemático y teólogo italiano Luca Pacioli publicó un libro titulado 'La divina proporción', en el que daba cinco razones por las que el número áureo debía considerarse divino:
a) La unidad del número, que se asemeja a Dios.
b) El hecho de que esté definido por tres segmentos de una recta, que se asemeje a la Trinidad.
c) La inconmensurabilidad del número, igual que Dios es inconmensurable.
d) Este número es omnipresente e invariable, igual que Dios.
e) Dios dio ser al universo a través de la quintaesencia, representada por un dodecaedro, y el número áureo dio ser al dodecaedro.
Los estudios previos de Abu Kamil influyeron en Leonardo de Pisa (Fibonacci), que los empleó para resolver problemas geométricos, pero no llegó a conectarlos con la famosa secuencia que posteriormente fue nombrada en su honor.
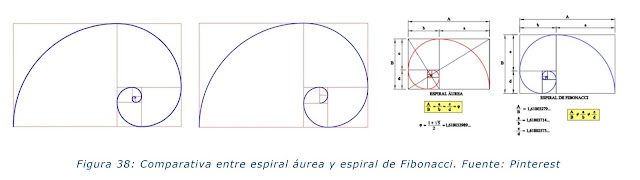
En 1525, Alberto Durero publicó 'Instrucción sobre la medida con regla y compás de figuras planas' sólidas', donde describe cómo trazar la espiral basada en la proporción áurea, denominada espiral áurea o espiral de Durero.
Johannes Kepler (1571-1630) incluyó en su tratado 'El misterio cósmico', sobre la concepción de un modelo platónico del Sistema Solar -empleando los sólidos platónicos-, la siguiente frase respecto del número áureo: “La geometría tiene dos grandes tesoros: uno, el teorema de Pitágoras; el otro, la división de una línea entre el extremo y su proporcional.
El primero lo podemos comparar a una medida de plata; el segundo lo debemos denominar una joya preciosa”. La primera aproximación decimal al número áureo la consiguió Michael Maestlin en 1597, obteniendo un valor de 0,6180340.
El primer uso conocido del adjetivo áureo, dorado o de oro para referirse a este número se debe al El matemático alemán Martin Ohm (hermano del célebre físico Georg Simon Ohm). Martín, en la segunda edición de 1835 de su libro 'Las matemáticas puras elementales', escribe una nota al pie que aclara: 'Uno también acostumbra llamar a esta división de una línea arbitraria en dos partes como éstas la sección dorada'.
Esta referencia parece implicar que el término ya era de uso común en ese año. Tal vez el hecho de que en la primera edición del libro no se incluye esta nota sugiere que comenzó a hacerse muy popular en la década de 1830.
En el siglo XVIII Abraham de Moivre, Daniel Bernoulli y Leonhard Euler emplearon una fórmula para relacionar la secuencia de Fibonacci y el número áureo. En 1843 fue redescubierta por Jacques Binet, dando nombre a la fórmula.
Actualmente el número áureo se designa con la letra phi (Φ), desde que en 1910 el matemático Mark Barr le adjudicó esta denominación en honor al escultor griego Fidias, por el máximo valor estético atribuido a su escultura y porque se cree empleaba ya esta proporción en la antigüedad.
.PARA OBTENER EL DOCUMENTO COMPLETO
FUENTE DE INFORMACIÓN
https://www.acta.es/medios/articulos/matematicas/119001.pdf






























No hay comentarios:
Publicar un comentario