INTRODUCCIÓN
El ser humano ha sentido a lo largo de la historia un elevado interés por el número áureo, asociándolo con el ideal de belleza y otorgándole una importancia mística.
Descubierto en las civilizaciones antiguas como una proporción geométrica tal que a la percepción cerebro humano le resulta especialmente agradable, sus propiedades matemáticas de autosemejanza, homotecia y fractalidad le confieren un papel fundamental en la naturaleza, apareciendo en multitud de circunstancias realmente asombrosas y fascinantes.
Tal es así que para muchos estudiosos de la materia el número áureo es considerado como el número asociado a la creación.
CONCEPTO
Geométricamente, y tal y como lo definió Euclides -considerado el padre de la geometría-, el número áureo es el valor numérico de la proporción que guardan entre sí dos segmentos de recta a y b (siendo a más largo que b), tales que la longitud total (suma de los dos segmentos ayb) es al segmento mayor a como el segmento mayor a es al segmento menor b. Es decir, el total es a la parte mayor, como la mayor es la pequeña.
APARICIÓN EN LA NATURALEZA
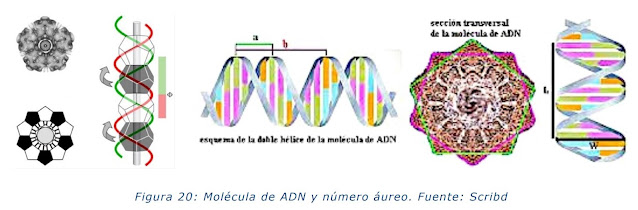
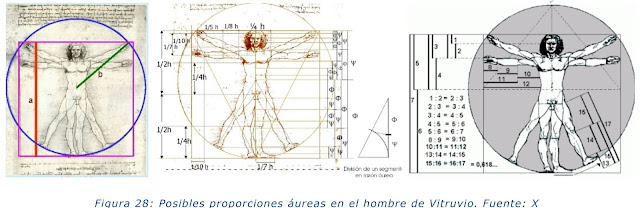
El número áureo y la sucesión de Fibonacci aparecen de forma natural en la morfología y el crecimiento evolutivo de los seres vivos. Aparece en los patrones de crecimiento y supervivencia de las plantas, en Múltiples proporciones del hombre y del reino animal, e incluso es la base de la formación de la molécula de la vida, el ADN.
APARICIÓN EN LAS PLANTAS. FILOTAXIS
La filotaxis o filotaxia es la rama de la botánica que se encarga del estudio de la disposición de tallos, ramas, hojas y flores en las plantas. En este ámbito el número áureo y la sucesión de Fibonacci aparece en innumerables ocasiones, lo que para muchos investigadores demuestra que el número áureo es al crecimiento orgánico lo que el número PI (3.1416...) es a la medición del círculo: es el número en el que están basados todos los cálculos y fenómenos de crecimiento de los seres vivos.
En concreto, el número áureo y la sucesión de Fibonacci aparecen en las plantas en el número y disposición y grosor de ramas; el número, disposición y forma de hojas; el número, disposición y forma de flores y sus componentes; el número, y en la forma y distribución de frutos y semillas.
Específicamente, en la adopción de determinados patrones de distribución juega un papel fundamental el ángulo áureo, que no es más que la razón áurea aplicada a una circunferencia.
En el número de pétalos de las flores, por ejemplo, es muy habitual encontrar números de Fibonacci. Los más típicos son 5 y 8, aunque también las hay de 13, 21, 34, 55, 89 y 144, no habiéndolas por ejemplo de 33, 35, 20 ó 24.
Esta misma aparición de los números de Fibonacci ocurre también en las distintas partes de la flor, pudiendo tener un número de Fibonacci para los pétalos, otro distinto para los sépalos, y otro distinto para los estambres. Es lo que ocurre por ejemplo con la flor de la fruta de la pasión, y con otras muchas plantas. A nivel morfológico también la forma de las hojas y las distancias entre ellas en el tallo siguen proporciones basadas en el número áureo.
Por su parte, el número de ramas y el número de hojas también es muy común que siga un patrón de Fibonacci, proporcionando formas muy características en el crecimiento de árboles y arbustos.
En las escalas de una piña, o de una alcachofa, también aparecen diversas espirales según números de la sucesión de Fibonacci. Lo habitual en las plantas es que dispongan sus elementos optimizando el espacio, de forma que se maximice la luz solar recibida (hojas) y se exponga un mayor número de elementos (flores, semillas).
Así, para que las hojas de una planta o las ramas alrededor de un tronco reciban la máxima luz solar posible, estos elementos deben estar distribuidos de forma que tengan la mínima interferencia entre ellos. Para ello, en la situación ideal deben crecer verticalmente en hélice ascendente según un ángulo constante igual al ángulo áureo. Este hecho fue descubierto empíricamente por Church, y confirmado matemáticamente por Weisner en 1875.
Las plantas crecen a partir de un pequeño grupo de células -denominado meristema- y situadas en la punta de cada sección que crece: ramas, brotes, pétalos, etc. Las células crecen y se ordenan en espiral, cada una apuntando a una dirección manteniendo un cierto ángulo respecto del punto central. Asombrosamente, con un único ángulo (el ángulo áureo), la planta puede organizar su propio diseño de forma óptima, sin que importe cuánto más va a crecer la planta. Esto aplica a ramas, hojas, pétalos, semillas y cualquier otra parte de la planta.
Un caso espectacular de este fenómeno lo constituye la distribución de las semillas en el girasol el algoritmo para el patrón de distribución de los flosculos (semillas) fue propuesto por Helmut Vogel en 1979, determinando un ángulo para cada semilla de Θ = n Φ y una distancia al centro de r = c√n. El ángulo Φ de divergencia es el ángulo áureo (137,508º, o 222,492º en sentido contrario), y en cada paso se va ubicando una semilla rellenando, de forma óptima, todo el espacio.
En general, los ángulos que sean divisores de los 360º (0º, 45º, 60º, 90º, 180º, etc.) se aprovechan muy mal el espacio, ya que repetirán muchas posiciones. Incluso ángulos con una diferencia de décimas de grado producen patrones completamente distintos. Notese que el aprovechamiento del espacio sólo es óptimo para el ángulo áureo y su complementario, con la única diferencia entre ambos del sentido de ubicación de las semillas.
Aplicando este algoritmo con el valor óptimo del ángulo áureo, además de maximizarse el aprovechamiento del espacio, vuelven a aparecer una vez más los números de Fibonacci. En la distribución así obtenido aparecen 3 tipologías de espirales (denominadas espirales de Fermat) en el patrón, cada una de ellas según un número de Fibonacci de veces.
Una última curiosidad sobre el número áureo en las plantas. En algunas familias, específicamente de plantas crasas y cactáceas, es habitual encontrarse distribuciones morfológicas según la sucesión de Lucas (similar a la de Fibonacci y tendiendo igualmente al número áureo entre valores consecutivos, pero con diferentes valores iniciales: 2, 1, 3, 4, 7, 11, 18, etc.).
FUENTE DE INFORMACIÓN
https://www.acta.es/medios/articulos/matematicas/120001.pdf






























No hay comentarios:
Publicar un comentario