RETICULAS ESPACIALES
Toda la materia de nuestro mundo se organiza en estructuras de complejidad creciente, a partir de elementos más simples: quarks, partículas elementales, átomos, moléculas, ADN, ARN, proteínas, virus, cristales, plantas, animales... Las propiedades de las estructuras derivadas son diferentes de las de los elementos constituyentes. La forma que adopta la materia es el resultado de la cooperación entre sus partes (fuerzas físicas, químicas ...), y crea un nuevo orden, novedad estructural y funcional.
El conocimiento de la arquitectura de un elemento nos permite comprender y predecir algunos aspectos de su comportamiento. Ejemplo: el diseño racional de medicamentos se basa en su estructura.
La retícula es un concepto clave para analizar las formas de los cuerpos y para construirlos. En las retículas más sencillas se repiten uno o varios módulos. Los módulos que ocupan el espacio, sin dejar huecos, decimos que lo macizan o empaquetan. En el caso del plano, diremos que lo teselan o pavimentan. Ejemplo: los cuadrados pavimentan el plano y los cubos macizan el espacio.
Las retículas se presentan en la naturaleza, en la tecnología o en el arte, como armaduras que sostienen un cuerpo, como asociaciones modulares o como grietas en una superficie.
La lista de retículas en la naturaleza es interminable: celdillas hexagonales de las colmenas, prismas hexagonales del basalto y del coral, células de la sangre o del cerebro, capa epidérmica de los animales, escamas de peces y reptiles, alas de libélula, cristales...
En la tecnología y en el arte son también numerosos los ejemplos: tramas de películas fotográficas digitalizadas, grabados, dispersión por agua del colorante, espuma de jabón, mosaicos, alambradas, muros, estructuras de edificios...
Con frecuencia, la materia adopta formas poliédricas, de caras poligonales. Los poliedros serán los ladrillos con los que construiremos las retículas.
Nuestra intención con esta exposición es mostrar modelos de estructuras reticulares de la materia y ofrecer un entorno apropiado para descubrir el orden, la belleza y la sorpresa que encierra.
Eliseo Borrás
Este texto introducía la exposición De Natura Reticular celebrada en 2004 en la sala de exposiciones del Jardín Botánico de la Universidad de Valencia y coordinada por el autor del texto, Eliseo, físico-matemático y amigo.
El título de la exposición tenía un doble sentido, por un lado hacía referencia a la génesis de las retículas espaciales, como y porque se forman, tema que nos ocupa en este apartado. Por otro, mostraba ejemplos mediante fotografías de Pilar Moreno de retículas que podemos descubrir y estudiar en la Naturaleza: una red de tela de araña, celdillas de abejas, retículado de la piel de la jirafa, ramificaciones,…
Realmente se podría decir que sobre geometría está, desde hace tiempo, todo dicho. La novedad residirá pues, en la forma de decirlo. La utilización de recortables para construir “imágenes reales tangibles”, valga la contradicción en este caso, pues nunca una imagen es tangible. La “imagen dibujada”, “imagen fotográfica”, en estos casos valga la redundancia. “Imagen virtual” de las nuevas tecnologías.
Todas ellas aportarán un punto de vista diferente y propio para cada ocasión. Y ¿por qué los estudios sobre geometría carecen de color? No existe un mundo en blanco y negro; toda forma tiene su color, el agua, el aire, los cristales, tienen el color de aquello que transparentan o reflejan. Y, al contrario, todo color está contenido en una forma, como todo sonido tiene una duración en el tiempo (ritmo) o toda palabra tiene su significado. La utilización del color nos ayudará a la mejor comprensión de la forma. Con la impresión digital esto ya es posible sin un mayor esfuerzo.
RETICULAS POLIEDRICAS
Si en las retículas planas la condición para teselar el plano era sumar ángulos de polígonos hasta los 360º, igual será para las retículas espaciales, sumando en este caso ángulos diedros de caras iguales de poliedros.
Evidentemente, cualquier extrusión de una retícula plana rellenará también el espacio tridimensional, pues serían prismas de distinta base poligonal. Es el caso del cubo, pues todos sus ángulos diedros son 90º. No sucederá así con los demás poliedros que conforman las distintas retículas.
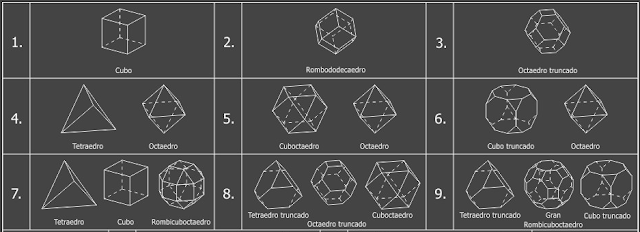
Diez son los poliedros que ya solos o en grupos de dos o tres rellenarán el espacio, ellos conformarán once formaciones reticulares distintas cuya particularidad es que todas sus partes proceden del cubo y en su convexidad total macizarán también un espacio cúbico.
Otras dos retículas, descritas finalmente, tienen la particularidad de no hacerlo. En su convexidad reticular una rellenará la mínima parte espacial: un tetraedro. La otra, formada por hexaedros de rombos áureos, completará la forma poliédrica más compleja: el triacontaedro rómbico. En total serán trece las retículas poliédricas que a continuación se detallan.
Se describen a continuación la génesis de las retículas espaciales formadas por poliedros regulares y semirregulares, además mediante el siguiente programa pueden visualizarse en tres dimensiones las retículas presentadas.
Requerimientos mínimos:
Windows XP, Vista o 7.
Microsoft .NET framework 4.0
Una tarjeta gráfica con soporte para OpenGL.
Descargas
Ingresar a la pagina delautor:
Información extraida de:

















1 comentario:
Hola amigos/as de apuntes de arquitectura, gracias por esta publicación. Estuve accediendo al blog de donde obtuvieron este contenido durante los dos últimos años y hace unos meses me encuentro con que no esta mas la pagina www.formaynumero.webuda.com. Como sabrán había muuucha información interesante y muy bien presentada allí. Pregunto si no tendrán alguna idea de como contactar a los autores??? mil gracias y saludos. José
Publicar un comentario